Choose any three.
|
|
SQL As Understood By SQLite
WITH clause
Common Table Expressions or CTEs act like temporary views that exist only for the duration of a single SQL statement. There are two kinds of common table expressions: "ordinary" and "recursive". Ordinary common table expressions are helpful for making queries easier to understand by factoring subqueries out of the main SQL statement. Recursive common table expressions provide the ability to do hierarchical or recursive queries of trees and graphs, a capability that is not otherwise available in the SQL language.
All common table expressions (ordinary and recursive) are created by prepending a WITH clause in front of a SELECT, INSERT, DELETE, or UPDATE statement. A single WITH clause can specify one or more common table expressions, some of which are ordinary and some of which are recursive.
Ordinary Common Table Expressions
An ordinary common table expression works as if it were a view that exists for the duration of a single statement. Ordinary common table expressions are useful for factoring out subqueries and making the overall SQL statement easier to read and understand.
A WITH clause can contain ordinary common table expressions even if it includes the RECURSIVE keyword. The use of RECURSIVE does not force common table expressions to be recursive.
Recursive Common Table Expressions
A recursive common table expression can be used to write a query that walks a tree or graph. A recursive common table expression has the same basic syntax as an ordinary common table expression, but with the following additional features:
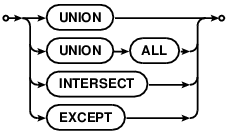
- The "select-stmt" must be a compound select where the right-most compound-operator is either UNION or UNION ALL.
- The table named on the left-hand side of the AS keyword must appear exactly once in the FROM clause of the right-most SELECT statement of the compound select, and nowhere else.
To put it another way, a recursive common table expression must look like the following:
We refer to the table named by the cte-table-name in a recursive common table expression as the "recursive table". In the recursive-cte bubble diagram above, the recursive table must appear exactly once in the FROM clause of the recursive-select and must not appear anywhere else in either the initial-select or the recursive-select, including subqueries. The initial-select may be a compound select, but it may not include an ORDER BY, LIMIT, or OFFSET. The recursive-select must be a simple select, not a compound. The recursive-select is allowed to include an ORDER BY, LIMIT, and/or OFFSET.
The basic algorithm for computing the content of the recursive table is as follows:
- Run the initial-select and add the results to a queue.
- While the queue is not empty:
- Extract a single row from the queue.
- Insert that single row into the recursive table
- Pretend that the single row just extracted is the only row in the recursive table and run the recursive-select, adding all results to the queue.
The basic procedure above may modified by the following additional rules:
If a UNION operator connects the initial-select with the recursive-select, then only add rows to the queue if no identical row has been previously added to the queue. Repeated rows are discarded before being added to the queue even if the repeated rows have already been extracted from the queue by the recursion step. If the operator is UNION ALL, then all rows generated by both the initial-select and the recursive-select are always added to the queue even if they are repeats. When determining if a row is repeated, NULL values compare equal to one another and not equal to any other value.
The LIMIT clause, if present, determines the maximum number of rows that will ever be added to the recursive table in step 2b. Once the limit is reached, the recursion stops. A limit of zero means that no rows are ever added to the recursive table, and a negative limit means an unlimited number of rows may be added to the recursive table.
The OFFSET clause, if it is present and has a positive value N, prevents the first N rows from being added to the recursive table. The first N rows are still processed by the recursive-select; they just are not added to the recursive table. Rows are not counted toward fulfilling the LIMIT until all OFFSET rows have been skipped.
If an ORDER BY clause is present, it determines the order in which rows are extracted from the queue in step 2a. If there is no ORDER BY clause, then the order in which rows are extracted is undefined. (In the current implementation, the queue becomes a FIFO if the ORDER BY clause is omitted, but applications should not depend on that fact since it might change.)
Recursive Query Examples
The following query returns all integers between 1 and 1000000:
WITH RECURSIVE cnt(x) AS (VALUES(1) UNION ALL SELECT x+1 FROM cnt WHERE x<1000000) SELECT x FROM cnt;
Consider how this query works. The initial-select runs first and returns a single row with a single column "1". This one row is added to the queue. In step 2a, that one row is extracted from the queue and added to "cnt". Then the recursive-select is run in accordance with step 2c generating a single new row with value "2" to add to the queue. The queue still has one row, so step 2 repeats. The "2" row is extracted and added to the recursive table by steps 2a and 2b. Then the row containing 2 is used as if it were the complete content of the recursive table and the recursive-select is run again, resulting in a row with value "3" being added to the queue. This repeats 999999 times until finally at step 2a the only value on the queue is a row containing 1000000. That row is extracted and added to the recursive table. But this time, the WHERE clause causes the recursive-select to return no rows, so the queue remains empty and the recursion stops.
Optimization note: In the discussion above, statements like "insert the row into the recursive table" should be understood conceptually, not literally. It sounds as if SQLite is accumulating a huge table containing one million rows, then going back and scanning that table from top to bottom to generate the result. What really happens is that the query optimizer sees that values in the "cnt" recursive table are only used once. So as each row is added to the recursive table, that row is immediately returned as a result of the main SELECT statement and then discarded. SQLite does not accumulate a temporary table containing a million rows. Very little memory is needed to run the above example. However, if the example had used UNION instead of UNION ALL, then SQLite would have had to keep around all previously generated content in order to check for duplicates. For this reason, programmers should strive to use UNION ALL instead of UNION when feasible.
Here is a variation on the previous example:
WITH RECURSIVE
cnt(x) AS (
SELECT 1
UNION ALL
SELECT x+1 FROM cnt
LIMIT 1000000
)
SELECT x FROM cnt;
There are two differences in this variation. The initial-select is "SELECT 1" instead of "VALUES(1)". But those are just different syntaxes for saying exactly the same thing. The other change is that the recursion is stopped by a LIMIT rather than a WHERE clause. The use of LIMIT means that when the one-millionth row is added to the "cnt" table (and returned by the main SELECT, thanks to the query optimizer) then the recursion stops immediately regardless of how many rows might be left in the queue. On more complex queries, it can sometimes be difficult to ensure that the WHERE clause will eventually cause the queue to drain and the recursion to terminate. But the LIMIT clause will always stop the recursion. So it is good practice to always include a LIMIT clause as a safety if an upper bound on the size of the recursion is known.
Hierarchical Query Examples
Consider a table that describes the members of an organization as well as the chain-of-command within that organization:
CREATE TABLE org( name TEXT PRIMARY KEY, boss TEXT REFERENCES org, height INT, -- other content omitted );
Every member in the organization has a name, and most members have a single boss. (The head of the whole organization has a NULL "boss" field.) The rows of the "org" table form a tree.
Here is a query that computes the average height over everyone in Alice's organization, including Alice:
WITH RECURSIVE
works_for_alice(n) AS (
VALUES('Alice')
UNION
SELECT name FROM org, works_for_alice
WHERE org.boss=works_for_alice.n
)
SELECT avg(height) FROM org
WHERE org.name IN works_for_alice;
The next example uses two common table expressions in a single WITH clause. The following table records a family tree:
CREATE TABLE family( name TEXT PRIMARY KEY, mom TEXT REFERENCES family, dad TEXT REFERENCES family, born DATETIME, died DATETIME, -- NULL if still alive -- other content );
The "family" table is similar to the earlier "org" table except that now there are two parents to each member. We want to know all living ancestors of Alice, from oldest to youngest. An ordinary common table expression, "parent_of", is defined first. That ordinary CTE is a view that can be used to find all parents of any individual. That ordinary CTE is then used in the "ancestor_of_alice" recursive CTE. The recursive CTE is then used in the final query:
WITH RECURSIVE
parent_of(name, parent) AS
(SELECT name, mom FROM family UNION SELECT name, dad FROM family),
ancestor_of_alice(name) AS
(SELECT parent FROM parent_of WHERE name='Alice'
UNION ALL
SELECT parent FROM parent_of JOIN ancestor_of_alice USING(name))
SELECT family.name FROM ancestor_of_alice, family
WHERE ancestor_of_alice.name=family.name
AND died IS NULL
ORDER BY born;
Queries Against A Graph
A version control system (VCS) will typically store the evolving versions of a project as a directed acyclic graph (DAG). Call each version of the project a "checkin". A single checkin can have zero or more parents. Most checkins (except the first) have a single parent, but in the case of a merge, a checkin might have two or three or more parents. A schema to keep track of checkins and the order in which they occur might look something like this:
CREATE TABLE checkin( id INTEGER PRIMARY KEY, mtime INTEGER -- timestamp when this checkin occurred ); CREATE TABLE derivedfrom( xfrom INTEGER NOT NULL REFERENCES checkin, -- parent checkin xto INTEGER NOT NULL REFERENCES checkin, -- derived checkin PRIMARY KEY(xfrom,xto) ); CREATE INDEX derivedfrom_back ON derivedfrom(xto,xfrom);
This graph is acyclic. And we assume that the mtime of every child checkin is no less than the mtime of all its parents. But unlike the earlier examples, this graph might have multiple paths of differing lengths between any two checkins.
We want to know the twenty most recent ancestors in time (out of the thousands and thousands of ancestors in the whole DAG) for checkin "@BASELINE". (A query similar to this is used by the Fossil VCS to show the N most recent ancestors of a check. For example: http://www.sqlite.org/src/timeline?p=trunk&n=30.)
WITH RECURSIVE
ancestor(id,mtime) AS (
SELECT id, mtime FROM checkin WHERE id=@BASELINE
UNION
SELECT derivedfrom.xfrom, checkin.mtime
FROM ancestor, derivedfrom, checkin
WHERE ancestor.id=derivedfrom.xto
AND checkin.id=derivedfrom.xfrom
ORDER BY checkin.mtime DESC
LIMIT 20
)
SELECT * FROM checkin JOIN ancestor USING(id);
The "ORDER BY checkin.mtime DESC" term in the recursive-select makes the query run much faster by preventing it from following branches that merge checkins from long ago. The ORDER BY forces the recursive-select to focus on the most recent checkins, the ones we want. Without the ORDER BY on the recursive-select, one would be forced to compute the complete set of thousands of ancestors, sort them all by mtime, then take the top twenty. The ORDER BY essentially sets up a priority queue that forces the recursive query to look at the most recent ancestors first, allowing the use of a LIMIT clause to restrict the scope of the query to just the checkins of interest.
Controlling Depth-First Versus Breadth-First Search Of a Tree Using ORDER BY
An ORDER BY clause on the recursive-select can be used to control whether the search of a tree is depth-first or breadth-first. To illustrate, we will use a variation on the "org" table from an example above, without the "height" column, and with some real data inserted:
CREATE TABLE org(
name TEXT PRIMARY KEY,
boss TEXT REFERENCES org
) WITHOUT ROWID;
INSERT INTO org VALUES('Alice',NULL);
INSERT INTO org VALUES('Bob','Alice');
INSERT INTO org VALUES('Cindy','Alice');
INSERT INTO org VALUES('Dave','Bob');
INSERT INTO org VALUES('Emma','Bob');
INSERT INTO org VALUES('Fred','Cindy');
INSERT INTO org VALUES('Gail','Cindy');
Here is a query to show the tree structure in a breadth-first pattern:
WITH RECURSIVE
under_alice(name,level) AS (
VALUES('Alice',0)
UNION ALL
SELECT org.name, under_alice.level+1
FROM org JOIN under_alice ON org.boss=under_alice.name
ORDER BY 2
)
SELECT substr('..........',1,level*3) || name FROM under_alice;
The "ORDER BY 2" (which means the same as "ORDER BY under_alice.level+1") causes higher levels in the organization chart (with smaller "level" values) to be processed first, resulting in a breadth-first search. The output is:
Alice ...Bob ...Cindy ......Dave ......Emma ......Fred ......Gail
But if we change the ORDER BY clause to add the "DESC" modifier, that will cause lower levels in the organization (with larger "level" values) to be processed first by the recursive-select, resulting in a depth-first search:
WITH RECURSIVE
under_alice(name,level) AS (
VALUES('Alice',0)
UNION ALL
SELECT org.name, under_alice.level+1
FROM org JOIN under_alice ON org.boss=under_alice.name
ORDER BY 2 DESC
)
SELECT substr('..........',1,level*3) || name FROM under_alice;
The output of this revised query is:
Alice ...Bob ......Dave ......Emma ...Cindy ......Fred ......Gail
When the ORDER BY clause is omitted from the recursive-select, the queue behaves as a FIFO, which results in a breadth-first search.
Outlandish Recursive Query Examples
The following query computes an approximation of the Mandelbrot Set and outputs the result as ASCII-art:
WITH RECURSIVE
xaxis(x) AS (VALUES(-2.0) UNION ALL SELECT x+0.05 FROM xaxis WHERE x<1.2),
yaxis(y) AS (VALUES(-1.0) UNION ALL SELECT y+0.1 FROM yaxis WHERE y<1.0),
m(iter, cx, cy, x, y) AS (
SELECT 0, x, y, 0.0, 0.0 FROM xaxis, yaxis
UNION ALL
SELECT iter+1, cx, cy, x*x-y*y + cx, 2.0*x*y + cy FROM m
WHERE (x*x + y*y) < 4.0 AND iter<28
),
m2(iter, cx, cy) AS (
SELECT max(iter), cx, cy FROM m GROUP BY cx, cy
),
a(t) AS (
SELECT group_concat( substr(' .+*#', 1+min(iter/7,4), 1), '')
FROM m2 GROUP BY cy
)
SELECT group_concat(rtrim(t),x'0a') FROM a;
In this query, the "xaxis" and "yaxis" CTEs define the grid of points for which the Mandelbrot Set will be approximated. Each row in the "m(iter,cx,cy,x,y)" CTE means that after "iter" iterations, the Mandelbrot iteration starting at cx,cy has reached point x,y. The number of iterations in this example is limited to 28 (which severely limits the resolution of the computation, but is sufficient for low-resolution ASCII-art output). The "m2(iter,cx,cy)" CTE holds the maximum number of iterations reached when starting at point cx,cy. Finally, each row in the "a(t)" CTE holds a string which is a single line of the output ASCII-art. The SELECT statement at the end just queries the "a" CTE to retrieve all lines of ASCII-art, one by one.
Running the query above in an SQLite command-line shell results in the following output:
....#
..#*..
..+####+.
.......+####.... +
..##+*##########+.++++
.+.##################+.
.............+###################+.+
..++..#.....*#####################+.
...+#######++#######################.
....+*################################.
#############################################...
....+*################################.
...+#######++#######################.
..++..#.....*#####################+.
.............+###################+.+
.+.##################+.
..##+*##########+.++++
.......+####.... +
..+####+.
..#*..
....#
+.
This next query solves a Sudoku puzzle. The state of the puzzle is defined by an 81-character string formed by reading entries from the puzzle box row by row from left to right and then from top to bottom. Blank squares in the puzzle are denoted by a "." character. Thus the input string:
53..7....6..195....98....6.8...6...34..8.3..17...2...6.6....28....419..5....8..79
Corresponds to a puzzle like this:
5 3 7 6 1 9 5 9 8 6 8 6 3 4 8 3 1 7 2 6 6 2 8 4 1 9 5 8 7 9
This is the query that solves the puzzle:
WITH RECURSIVE
input(sud) AS (
VALUES('53..7....6..195....98....6.8...6...34..8.3..17...2...6.6....28....419..5....8..79')
),
digits(z, lp) AS (
VALUES('1', 1)
UNION ALL SELECT
CAST(lp+1 AS TEXT), lp+1 FROM digits WHERE lp<9
),
x(s, ind) AS (
SELECT sud, instr(sud, '.') FROM input
UNION ALL
SELECT
substr(s, 1, ind-1) || z || substr(s, ind+1),
instr( substr(s, 1, ind-1) || z || substr(s, ind+1), '.' )
FROM x, digits AS z
WHERE ind>0
AND NOT EXISTS (
SELECT 1
FROM digits AS lp
WHERE z.z = substr(s, ((ind-1)/9)*9 + lp, 1)
OR z.z = substr(s, ((ind-1)%9) + (lp-1)*9 + 1, 1)
OR z.z = substr(s, (((ind-1)/3) % 3) * 3
+ ((ind-1)/27) * 27 + lp
+ ((lp-1) / 3) * 6, 1)
)
)
SELECT s FROM x WHERE ind=0;
The "input" CTE defines the input puzzle. The "digits" CTE defines a table that holds all digits between 1 and 9. The work of solving the puzzle is undertaken by the "x" CTE. An entry in x(s,ind) means that the 81-character string "s" is a valid sudoku puzzle (it has no conflicts) and that the first unknown character is at position "ind", or ind==0 if all character positions are filled in. The goal, then, is to compute entries for "x" with an "ind" of 0.
The solver works by adding new entries to the "x" recursive table. Given prior entries, the recursive-select tries to fill in a single new position with all values between 1 and 9 that actually work in that position. The complicated "NOT EXISTS" subquery is the magic that figures out whether or not each candidate "s" string is a valid sudoku puzzle or not.
The final answer is found by looking for a string with ind==0. If the original sudoku problem did not have a unique solution, then the query will return all possible solutions. If the original problem was unsolvable, then no rows will be returned. In this case, the unique answer is:
534678912672195348198342567859761423426853791713924856961537284287419635345286179
The solution was computed in less than 300 milliseconds on a modern workstation.
Limitations And Caveats
The WITH clause cannot be used within a CREATE TRIGGER.
The WITH clause must appear at the beginning of a top-level SELECT statement or at the beginning of a subquery. The WITH clause cannot be prepended to the second or subsequent SELECT statement of a compound select.
The SQL:1999 spec requires that the RECURSIVE keyword follow WITH in any WITH clause that includes a recursive common table expression. However, for compatibility with SqlServer and Oracle, SQLite does not enforce this rule.